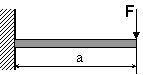Základy mechaniky - otázky.
1. Síla je jednoznačně určena, když známe:
a) Působiště a velikost.
b) Velikost a směrový úhel.
c) Velikost, jeden bod na nositelce a směrový úhel.
d) Nositelku a její směr.
2. Obecnou rovinnou silovou soustavu můžeme vždy uvést do rovnováhy:
a) Jednou silou procházející počátkem souřadného systému.
b) Silovou dvojicí.
c) Jednou silou, působící na správně určené nositelce.
d) Nejméně dvěma silami.
3. Pro polohu těžiště homogenních těles platí:
a) Je závislá na měrné hmotnosti materiálu tělesa.
b) Na Zemi i na Měsíci je stejná..
c) Nelze ji jednoznačně určit.
d) U dutých těles neexistuje.
a) Má 2 stupně volnosti.
b) Může se pohybovat.
c) Je uloženo staticky neurčitě.
d) Je uloženo staticky určitě.
a) Posouvající síla v místě vetknutí je rovna síle F.
b) Nosník není namáhán žádnou normálovou silou.
c) Průběh ohybového momentu je parabolický.
d) Ohybový moment v polovině délky nosníku je roven F·½·a.
6. Pro řešení staticky určitých soustav těles platí:
a) Potřebujeme tolik rovnic rovnováhy, kolik je neznámých vazbových sil.
b) Potřebujeme tolik rovnic rovnováhy, kolik je v soustavě těles.
c) Vazbové síly k řešení namáhání jednotlivých členů soustavy nepotřebujeme.
d) Rovnice rovnováhy celé soustavy nelze použít ani pro kontrolu.
a) Její velikost závisí na materiálu dotykových ploch.
b) Její velikost téměř nezáleží na rychlosti pohybujícího se tělesa.
c) Působí vždy proti pohybu.
d) Její velikost je stále stejná, i když je těleso v klidu.
a) Závisí na druhu materiálu.
b) Je to napětí, od kterého nastávají v materiálu plastické změny.
c) Udává maximální možné namáhání materiálu.
d) Její hodnota se zjišťuje tahavou zkouškou.
9. Pro řešení staticky neurčitých úloh platí:
a) Statické rovnice rovnováhy jsou nepoužitelné.
b) Potřebujeme tolik deformačních rovnic, kolik je neznámých vazbových sil.
c) Lze je řešit pouze při zatížení osamělou silou.
d) Potřebujeme tolik deformačních rovnic, kolikrát je úloha staticky neurčitá.
10. Tenzor napětí pro dvojosý stav namáhání obsahuje:
a) hodnotu maximálního napětí,
b) 2 různé hodnoty napětí,
c) 3 různé hodnoty napětí,
d) 6 různých hodnot napětí.
11. Když při pohybu bereme v úvahu odpor prostředí závislý na rychlosti, jde o pohyb:
a) nerovnoměrný,
b) rovnoměrně zrychlený,
c) rovnoměrný,
d) rovnoměrně zpomalený.
12. Hmotný bod se pohybuje přímočarým rovnoměrně zrychleným pohybem, když:
a) Součet sil na něj působících je funkcí času.
b) Na něj působí pouze jedna síla.
c) Součet sil na něj působících je konstantní.
d) Na něj nepůsobí žádná síla.
13. Velikost normálového zrychlení při pohybu bodu po kružnici je dána:
a) Jen rychlostním stavem bodu.
b) Tím, nakolik bod zrychluje.
c) Jen poloměrem kružnice, po které se bod pohybuje.
d) Ani jedna z předchozích odpovědí není správná.
14. Pro posuvný pohyb tělesa vždy platí:
a) Trajektorie všech bodů tělesa jsou ekvidistantní přímky.
b) Rychlosti všech bodů tělesa jsou stejné, zrychlení jsou různá.
c) Kinetickou energii tělesa můžeme určit pomocí rychlosti libovolného bodu a hmotnosti tělesa.
d) Součet sil působících na těleso je konstantní.
15. Síla je vektorová veličina. To znamená, že :
a) má pouze velikost,
b) má pouze směr,
c) má velikost a směr,
d) její velikost je rovna směru.
16. Těleso o hmotnosti m = 10 kg je k Zemi přitahováno tíhovou silou G :
a) G = 0,981 N,
b) G = 9,81 N,
c) G = 98,1 N,
d) G = 981 N.
17. Výslednice sil F1 a F2,
které spolu svírají úhel a, je 
. Její velikost je :
a) 
,
b) 
,
c) 
,
d) 
.
a) FV = 7 kN,
b) FV = 1 kN,
c) FV > 1 kN a zároveň FV < 7 kN,
d) FV = 5 kN.
19. Výslednice sil F1 a F2,
které jsou k sobě kolmé, je . Její velikost je :
a) ,
b) ,
c) 
,
d) 
.
20. Jsou-li Fx
a Fy x-ová a y-ová
složka síly F, pak úhel, který síla F svírá s osou x je :
a) 
,
b) 
,
c) 
,
d) 
.
21. Prostý součet sil lze použít tehdy :
a) jsou-li síly navzájem rovnoběžné,
b) jsou-li síly k sobě kolmé,
c) vždy,
d) nikdy.
a) přímka kolmá k síle,
b) přímka na níž leží vektor síly,
c) přímka která se silou F svírá
úhel ,
d) něco úplně jiného.
23. Moment síly má na těleso účinek :
a) posuvný,
b) otáčivý,
c) zvedající,
d) vzdalující.
24. Velikost momentu síly závisí na velikosti síly a :
a) na směru síly,
b) na působišti síly,
c) na vzdálenosti momentového bodu od nositelky síly,
d) na dráze síly.
25. Moment síly se vypočte jako :
a) součin velikosti síly a směru síly,
b) součin velikosti síly a ramene síly,
c) součin velikosti síly a dráhy síly,
d) součin x-ové a y-ové složky síly.
26. Rameno síly je :
a) vzdálenost momentového bodu od působiště síly,
b) vzdálenost počátečního a koncového bodu vektoru síly,
c) kolmá vzdálenost momentového bodu od nositelky síly,
d) vzdálenost působiště síly od počátku souřadného systému.
27. Jednotkou momentu síly je :
a) N,
b) kg,
c) N·m,
d) N/m.
a) dvě libovolné síly,
b) dvě síly k sobě kolmé,
c) dvě síly stejně velké, rovnoběžné, stejné orientace,
d) dvě síly stejně velké, rovnoběžné, opačné orientace.
29. Účinky silové dvojce jsou :
a) výsledný silový i momentový účinek jsou nulové,
b) výsledný silový účinek je nulový, výsledný momentový účinek je nenulový,
c) výsledný silový účinek je nenulový, výsledný momentový účinek je nulový,
d) výsledný silový i momentový účinek jsou nenulové.
30. Momentový účinek silové dvojce se vypočte jako :
a) součet obou sil,
b) součin obou sil,
c) součin síly a ramene silové dvojce,
d) součin síly a vzdálenosti působišť obou sil.
a) střední vzdálenost působišť obou sil od počátku souřadného systému,
b) kolmá vzdálenost mezi nositelkami obou sil,
c) vzdálenost středu mezi působišti obou sil od počátku souřadného systému,
d) vzdálenost mezi působišti obou sil.
32. Síla a moment síly k ose jsou veličiny :
a) veličiny vektorové,
b) veličiny skalární,
c) síla je veličina vektorová a moment síly k ose je veličina skalární,
d) síla je veličina skalární a moment síly k ose je veličina vektorová.
33. Těžiště je :
a) výslednice tíhových sil,
b) působiště výslednice tíhových sil,
c) rovnovážný bod,
d) středisko hmot.
34. Těžiště hmotné čáry (např. těleso vyrobené z drátu) :
a) existuje,
b) neexistuje,
c) existuje pouze je-li čára rovná,
d) existuje a musí ležet na této čáře (na drátu).
35. Těžiště hmotné plochy (např. výstřižek z plechu) :
a) existuje,
b) neexistuje,
c) existuje pouze je-li plocha rovinná,
d) existuje a musí ležet na této ploše.
a) existuje,
b) neexistuje,
c) existuje pouze je-li těleso homogenní,
d) existuje pouze je-li těleso nehmotné.
37. V čitateli výrazu pro výpočet x-ové souřadnice těžiště je :
a) celková tíha objektu - prostý součet tíhových sil jednotlivých dílčích objektů,
b) prostý součet součinů tíhových sil a x-ových souřadnic těžišť jednotlivých dílčích objektů,
c) prostý součet součinů tíhových sil a x-ových souřadnic jednotlivých bodů,
d) prostý součet součinů tíhových sil a kvadrátů x-ových souřadnic těžišť jednotlivých dílčích objektů.
38. Nosník je těleso, které po své délce :
a) může být zatíženo jen osamělými silami,
b) může být zatíženo jen ve vazbách,
c) může být zatíženo jen spojitým zatížením,
d) může být zatíženo zatížením kombinovaným.
a) možnost pohybovat se,
b) možný nezávislý pohyb,
c) možná vazba mezi dvěma tělesy,
d) možné silové působení mezi tělesy.
a) 2 stupně volnosti,
b) 3 stupně volnosti,
c) 6 stupňů volnosti,
d) 2 – 3 stupně volnosti.
a) silové působení mezi tělesy pouze v rovině,
b) mechanické spojení dvou těles,
c) bezkontaktní spojení dvou těles,
d) spojení dvou těles prostřednictvím třetího tělesa.
42. Pro prutovou soustavu platí :
a) nepředpokládá se žádné zjednodušení skutečné soustavy,
b) předpokládá se jen, že prutová soustava je tvořena z přímých prutů,
c) předpokládá se jen, že pruty jsou z ocele,
d) zavádí se zjednodušení : pruty nejsou zatíženy po své délce.
43. Pro styčníky prutové soustavy platí :
a) styčník je pevné spojení prutů,
b) zatížení nesmí být zavedeno do styčníku,
c) ve styčnících se předpokládá existence reálných vazeb - tj. vliv pasivních odporů apod.,
d) zavádí se zjednodušení : styčníky jsou ideální klouby, těžišťové osy prutů se ve styčníku sbíhají v jednom bodě.
44. Na velikost součinitele smykového tření f má vliv :
a) hmotnost tělesa,
b) velikost dotykové plochy,
c) drsnost dotýkajících se těles,
d) rychlost prokluzu těles.
45. Rychlost a zrychlení jsou veličiny :
a) vektorové,
b) skalární,
c) rychlost je veličina vektorová a zrychlení je veličina skalární,
d) rychlost je veličina skalární a zrychlení je veličina vektorová.
46. Rychlost je :
a) derivace dráhy podle času,
b) druhá derivace dráhy podle času,
c) derivace zrychlení podle dráhy,
d) derivace zrychlení podle času.
a) m/s2,
b) m·s,
c) m/s,
d) m.
48. Převádění jednotek. Rychlost v = 25 m/s je :
a) v = 9 km/hod,
b) v = 90 km/hod,
c) v = 900 km/hod,
d) v = 120 km/hod.
49. Při rovnoměrném pohybu tělesa je zrychlení a :
a) nenulové ve směru pohybu tělesa,
b) nenulové proti směru pohybu tělesa,
c) rovno nule,
d) nenulové ve směru výslednice soustavy zatěžujících sil.
a) pouze velikost hnací síly,
b) pouze poloha nositelky hnací síly,
c) pouze poloha těžiště tělesa,
d) jak velikost hnací síly a poloha její nositelky, tak poloha těžiště.
51. Při rotačním pohybu trajektorie všech bodů tělesa (při pohledu ve směru osy rotace) jsou :
a) kružnice o stejném poloměru a různých středech,
b) kružnice o různých poloměrech a různých středech,
c) kružnice o stejném poloměru se společným středem,
d) kružnice o různých poloměrech se společným středem (soustředné kružnice).
52. Otáčky tělesa n [ot/min] a úhlová rychlost w [rad/s] jsou :
a) dvě zcela odlišné veličiny,
b) platí převod w = 2·p·n/60,
c) platí převod n = 2·p·w/60,
d) jsou si rovny n = w.
53. Síla je :
a) skalár,
b) vektor vázaný na přímku,
c) tenzor 2. řádu,
d) volný vektor.
a) Pomyslná přímka, na které leží vektor síly.
b) Pomyslná přímka, která je rovnoběžná s vektorem síly.
c) Polopřímka , která je rovnoběžná s vektorem síly s počátkem v působišti.
d) Orientovaná úsečka jejíž jeden bod je působištěm síly a druhý závisí na velikosti síly.
a) N - newton,
b) kg - kilogram,
c) kg·m·s-2,
d) kg·m/s2.
56. Nenulový moment síly k nějaké ose má jen ta složka síly, jejíž nositelka :
a) Je s osou rovnoběžná.
b) Protíná osu.
c) Je kolmá na obě složky v odpovědích a) a b) a nemá s osou společný žádný bod.
d) Je s osou mimoběžná.
57. Vektor síly lze rozložit do maximálně kolika k sobě kolmých složek.
a) V rovině do 3 a v prostoru do 6 složek.
b) V rovině do 2 a v prostoru do 3 složek.
c) V rovině do 2 a v prostoru do 4 složek.
58. Rovnice rovnováhy pro prostorovou silovou soustavu se společným působištěm jsou :
a) SFx = 0 SFy = 0 SFz = 0 SMx = 0 SMy = 0 SMz = 0
b) SFx = 0 SFy = 0 SFz = 0
c) SFx = 0 SFy = 0 SMz = 0
a) žádnou silovou rovnici nelze nahradit,
b) pouze jednu silovou rovnici
lze nahradit rovnicí momentovou : 
, 
, 
c) obě silové rovnice lze
nahradit rovnicemi momentovými : , , 
d) obě silové rovnice lze
nahradit rovnicemi momentovými : , , , avšak momentové body nesmí ležet na jedné přímce.
a) M = Fx·xF + Fy·yF
b) 
c) M = Fy·xF - Fx·yF
d) Za zadaných hodnot nelze moment síly k počátku určit.
61. Pomocí Pappus - Guldinových vět nelze vypočíst objem a povrch :
a) kužele,
b) krychle,
c) koule,
d) válce.
62. Povrch koule je vytvořen rotací :
a) půlkružnice okolo osy o,
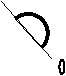
b) půlkružnice okolo osy b,
c) půlkruhu okolo osy o.
63. 
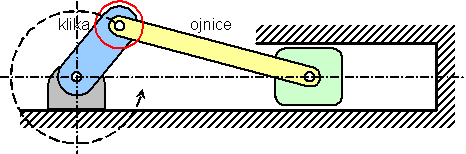Na obrázku je znázorněno schéma klikového mechanismu. Jaké
sílové účinky lze přenést vazbou mezi klikou a ojnicí (pasivní odpory zanedbáme)
?
a) Přenese se moment síly, který je záběrovým momentem motoru.
b) Přenese se pouze síla ve směru pohybu pístu (zde vodorovná).
c) Přenese se síla obecného směru (v rovině), kterou lze rozložit na dvě k sobě kolmé složky.
a) Pouze k počátku souřadné soustavy.
b) Ke všem bodům.
c) Stačí, že je nulový součet sil a z toho vyplývá, že je nulový i součet všech momentů.
a) 3 rovnice,
b) 6 rovnic,
c) 9 rovnic,
d) 12 rovnic.
66. Pohyblivá soustava těles (mechanismus) má počet stupňů volnosti :
a) menší než nula,
b) roven nule,
c) větší než nula,
d) větší nebo roven nule.
a) tah, tlak, krut,
b) tah, krut, ohyb,
c) tah, tlak, ohyb, smyk,
d) tah, ohyb, střih.
Zde T je posouvající síla, MO je ohybový moment,
x je podélná souřadnice. Jaký je možný průběh ohybového momentu a posouvající
síly pro konstantní posouvající sílu :a) Průběh A.
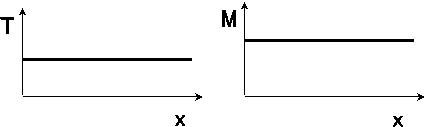
b) Průběh B.
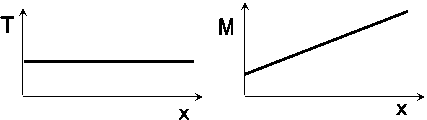
c) Průběh C.
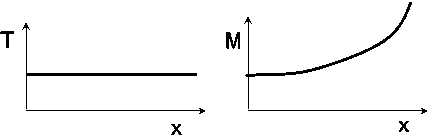
69. Normálová síla N má směr :
a) vodorovný,
b) ležící v rovině průřezu nosníku,
c) kolmý k průřezu nosníku,
d) kolmý na podélnou osu nosníku.
70. Sílu ve kterých prutech není možno přímo řešit metodou průsečnou :
a) v prutech 2,3,
b) v prutech 7,8,
c) v prutech 1,5,
d) v prutech 6,8.
71. Ve kterém případě lze danou soustavu řešit jako prutovou soustavu ?
a) ve všech nakreslených případech,
b) pouze zatížení A a zatížení B,
c) pouze zatížení A,
d) pouze zatížení A a zatížení C.
72. Modul pružnosti v tahu má velikost jako :
a) napětí, při kterém by se vzorek prodloužil na dvojnásobek své délky (za předpokladu že by v průběhu zatěžování stále platil Hookův zákon),
b) napětí na mezi úměrnosti,
c) napětí na mezi pevnosti,
d) maximální poměrná deformace.
a) Napsat momentové rovnice rovnováhy k dalším bodům.
b) Doplnit rovnice rovnováhy o deformační podmínky (jejich počet odpovídá stupni statické neurčitosti).
c) Reakce u takového tělesa nelze řešit.
74. Na obrázku jsou zobrazeny průběhy dráhy, rychlost a zrychlení bodu v závislosti na čase.
|
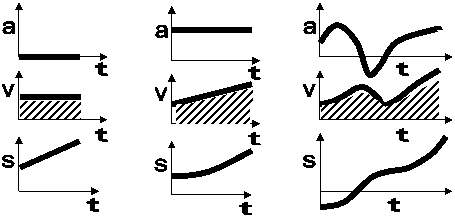
Pohyby bodu z časového hlediska |
pohyb rovnoměrný |
pohyb rovnoměrně zrychlený |
pohyb nerovnoměrný |
|
zrychlení |
a = 0 |
a = konst |
a ¹ konst |
|
rychlost |
v = konst |
v = a·t+v0 |
|
|
dráha |
s = v·t+s0 |
s = ½ a·t2+v0·t+s0 |
Vyšrafovaná plocha u průběhu rychlosti přestavuje :
a) přírůstek zrychlení od času t=0,
b) přírůstek rychlosti od času t=0,
c) přírůstek dráhy od času t=0,
d) přírůstek času od času t=0.
75. Těleso se pohybuje po přímce se zvyšujícím se zrychlením jestliže :
a) Na ně působí konstantní síla ve směru dráhy.
b) Na ně působí konstantní síla kolmo k dráze.
c) Na ně působí proměnná vzrůstající síla ve směru dráhy.
d) Na ně působí proměnná vzrůstající síla kolmo k dráze.
76. 
Jedete-li na ruském kole pak (za předpokladu
že nehybně sedíte v kabince) je váš pohyb :
a) rotační,
b) posuvný,
c) přímočarý,
d) obecný rovinný.
a) Jestliže projíždíte zatáčku dvakrát větší rychlostí a poloměr zatáčky je dvakrát větší.
b) Jestliže projíždíte zatáčku dvakrát větší rychlostí a poloměr zatáčky je dvakrát menší.
c) Jestliže projíždíte zatáčku stejnou rychlostí a poloměr zatáčky je čtyřikrát menší.
d) Jestliže projíždíte zatáčku dvakrát větší rychlostí a poloměr zatáčky je čtyřikrát větší.