Řešení a komentáře.

Špatné odpovědi jsou červené, správné odpovědi jsou zelené a podtržené.

50. Při pohybu tělesa pohybem posuvným přímočarým zrychleným má na stabilitu tělesa proti překlopení vliv :

a) pouze velikost hnací síly,

b) pouze poloha nositelky hnací síly,

c) pouze poloha těžiště tělesa,

d) jak velikost hnací síly a poloha její nositelky, tak poloha těžiště.

Jestliže na těleso, pohybující se posuvným přímočarým pohybem, působí dostatečně velká hnací síla F, pak se těleso bude pohybovat pohybem zrychleným.

Překročí-li hnací síla F jistou mez, dojde k překlopení tělesa.

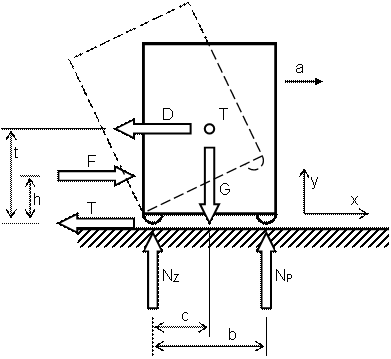
Na těleso působí :

Tíha G v těžišti,

hnací síla F ve svém působišti,

třecí síla T v místě podpor, proti směru pohybu,

normálové reakce N_P (přední) a N_Z (zadní) v místě podpor.

Bude-li hnací síla F dostatečně velké, avšak nepřekročí-li kritickou hodnotu, bude se těleso pohybovat posuvným přímočarým pohybem.

Z pohybové rovnice :

vyplývá zrychlení :

V místech podpor budou na těleso působit normálové reakce N_P (přední podpora) a N_Z (zadní podpora).

Pro tyto reakce platí rovnice rovnováhy :

N_Z + N_P = G

Tíhová síla se však na obě reakce rozdělí nerovnoměrně.

Bude-li se hnací síla F zvyšovat, bude se zadní reakce zvyšovat (přítlak na zadní podporu se bude zvyšovat),

naopak přední reakce se bude zmenšovat (přítlak na přední podporu se bude zmenšovat).

V kritickém okamžiku, těsně před překlopením, bude přední reakce nulová N_P = 0.

Chceme-li vyjádřit velikost přední reakce, musíme použít d’Alembertův princip.

Do těžiště zavedeme d’Alembertovu sílu

proti směru zrychlení.

Soustava sil, doplněná o d’Alembertovu sílu, musí být v rovnováze.

Po rozložení na složky :

První rovnice představuje pohybovou rovnici, druhá vyjadřuje celkovou velikost reakcí.

Chceme-li vyjádřit velikost přední reakce, musíme použít momentovou rovnici rovnováhy, např. k zadní podpoře :

kde b je vodorovná rozteč podpor,

c je vodorovný průmět vzdálenosti těžiště od zadní podpory,

h je výška působiště hnací síly nad podložkou,

t je výška těžiště nad podložkou.

Odtud :

Dále po dosazení

je

Vyjádříme-li dále třecí sílu (celkovou) jako :

kde f je koeficient tření, a je-li :

je přední reakce :

Jak již bylo uvedeno, v kritickém okamžiku, těsně před překlopením, bude přední reakce nulová N_P = 0.

neboli :

Je-li :

k překlopení nedojde.

Je-li naopak :

k překlopení dojde.

Je zřejmé, že stav podmínky pro překlopení (splněno nebo nesplněno)

závisí jak na velikosti hnací síly F (přesněji na jejím poměru k tíze G),

tak na poloze její nositelky (rozměr h),

tak na poloze těžiště (rozměry c a t).

Poznámka.

Řešení platí pro překlopení dozadu.

Nutnou podmínkou pro překlopení dozadu je t>h.

Pokud bude t<h nemůže dojít k překlopení dozadu.

Mohlo by dojít k překlopení dopředu.

V tom případě však budou silové poměry poněkud odlišné.

Pro vyšetření možnosti překlopení dopředu bychom museli provést celé řešení znovu.