Řešení a komentáře.

Špatné odpovědi jsou červené, správné odpovědi jsou zelené a podtržené.

56. Nenulový moment síly k nějaké ose má jen ta složka síly, jejíž nositelka:

a) Je s osou rovnoběžná.

b) Protíná osu.

c) Je kolmá na obě složky v odpovědích a) a b) a nemá s osou společný žádný bod.

d) Je s osou mimoběžná.

Vektor momentu síly v prostoru (3D) je dán vektorovým součinem :

kde je vektor síly a je polohový vektor působiště.

Nechceme-li používat vektorovou algebru, můžeme velikost momentu vyjádřit takto :

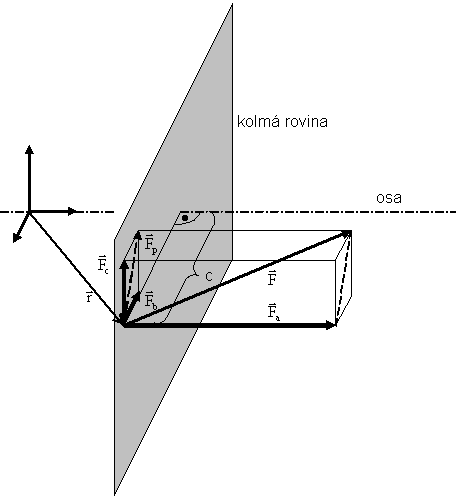
V působišti síly F vedeme rovinu kolmou k ose.

Sestrojíme průmět F_p síly F do této kolmé roviny.

Sílu F rozložíme na složky F_p v kolmé rovině a F_a rovnoběžně s osou.

Složku F_p dále rozložíme na složky F_b, jejíž nositelka protíná osu, a F_c, kolmá na F_b.

Síla je tedy rozložena na tři navzájem k sobě kolmé složky :

a) Složka F_a je s osou rovnoběžná. Její moment k ose je nulový.

b) Složka F_b je k ose kolmá a protíná ji. Působí tedy na nulovém rameni, její moment k ose je nulový.

c) Složka F_c je kolmá na složky F_a a F_b, s osou nemá žádný společný bod a je k ní kolmá.

Rameno síly F_c je c - kolmá vzdálenost působiště od osy, nebo také kolmá vzdálenost mezi osou a s ní rovnoběžnou složkou F_a.

M = F_c·c.

d) Celková síla F je s osou mimoběžná. Moment k ose však má pouze její složka F_c.