Řešení a komentáře.

Špatné odpovědi jsou červené, správné odpovědi jsou zelené a podtržené.

34. Těžiště hmotné čáry (např. těleso vyrobené z drátu) :

a) existuje,

b) neexistuje,

c) existuje pouze je-li čára rovná,

d) existuje a musí ležet na této čáře (na drátu).

Hmotné těleso, které má charakter čáry (např. je vyrobeno z drátu), je těleso „jako každé jiné“.

Má své těžiště - působiště výslednice tíhových sil.

Rozdělíme-li toto těleso na jistý počet dílčích těles (dílčích čar, dílčích drátů), pak souřadnice těžiště jsou :

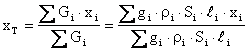
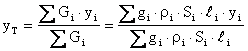
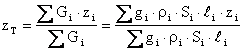
Zde G_i [N] je tíha i-té dílčí čáry, x_i, y_i, z_i [m] jsou souřadnice těžiště i-té dílčí čáry, g_i [m/s²]je gravitační zrychlení v těžišti i-té dílčí čáry, r_i [kg/m³] je měrná hmotnost (hustota) materiálu i-té dílčí čáry, S_i [m²] je příčný průřez i-té dílčí čáry, l_i [m] je délka i-té dílčí čáry.

Součin V_i = S_i·l_i [m³] je objem i-té dílčí čáry, součin m_i = r_i·V_i [kg] je hmotnost i-té dílčí čáry, konečně součin G_i = m_i·g_i [N] je tíha i-té dílčí čáry.

Je-li gravitační zrychlení g ve všech bodech stejné (což budou zřejmě všechny běžné technické případy), pak jej lze jak v čitateli, tak ve jmenovateli vytknout a následně vykrátit. Souřadnice těžiště pak budou :

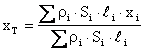
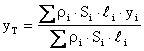
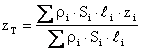
Je-li hustota r ve všech bodech stejná, pak ji lze jak v čitateli, tak ve jmenovateli vytknout a následně vykrátit. Souřadnice těžiště pak budou :

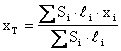
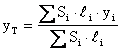
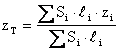
Konečně je-li příčný průřez S ve všech bodech stejný, pak jej lze jak v čitateli, tak ve jmenovateli vytknout a následně vykrátit. Souřadnice těžiště pak budou :

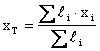
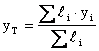
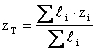
c) Čára, jejíž těžiště určujeme, může být libovolně zakřivená. Tvar však musí být jednoznačně definovaný.

d) Těžiště čáry nemusí ležet na samotné čáře.

Typickým příkladem je těžiště kružnice, které leží ve středu kružnice, nikoliv na jejím obvodu.